MESS: Manifold Embedding Motivated Super Sampling
Erik Thordsen and Erich Schubert
Motivation
Local intrinsic dimensionality estimation with Euclidean distance-based k-neighborhoods tends to give unstable results when using too few neighbors or too large neighborhood radii. Using too few neighbors is, e.g., prone to fluctuations in density and noise. Too large neighborhood radii can lead to including sections of the manifold that are geodesically distant, thereby raising the LID, or discarding small local features, thus lowering the LID. If possible, we would like to have more neighbors in small neighborhoods. By using locally linear approximations of the manifold’s embedding function from the δ-dimensional parameter space to the d-dimensional feature space, we hope to create additional on-manifold points.
Core Concept
We estimate local covariance matrices around all original points and generate supersamples from these distributions. In an additional step, the generated samples are pushed towards the manifold. If we generate, e.g., 50 points per original sample, we then have 50 times as many points in the same neighborhood radius as before and can perform LID estimation on much more points for the same appropriately small neighborhood size.
 |
 |
 |
Original data |
Raw supersamples |
Corrected supersamples |
Complementary Information
We currently know angle- and distance-based LID estimators but have not closed the gap between the two. Geometry-based supersampling features both aspects and can enrich both approaches. Geometric information is preserved in the sampling process and distance information are added as the geometry around distant points has less impact on local angle observations. By overlapping local supersampling distributions and correcting with a set of neighboring original points, the supersamples within a ball aggregate information from a larger environment. This adds additional information whilst not exceeding local geometry.
Linear Embedding Approximations
Assuming a locally linear manifold, and embedding function \(E: \mathbb{R}^\delta \to \mathbb{R}^d\) and its Jacobian \(\nabla E: \mathbb{R}^\delta \to \mathbb{R}^{d \times \delta}\) exist. Then for small ε:
\[Cov[E(B_\varepsilon(\tilde{x}))] \approx \frac{\varepsilon^2}{\delta + 2} \nabla E(\tilde{x})\nabla E(\tilde{x})^T\]for any \(\tilde{x}\) in the domain of E. That is, in the ideal case, local covariances yield information on the locally linear approximation \(\nabla E(\tilde{x})\) of E at \(\tilde{x}\). As covariance matrices are positive semidefinite and symmetric, all possible decompositions \(\Sigma = AA^T\) (e.g. Cholesky decomposition or Eigendecomposition) are equivalent up to rotation and reflection. So any spherically symmetric distribution behaves linearly transformed with any such decomposition in the same way as with \(\nabla E(\tilde{x})\).
Methods
The approach is - aside from the linear embedding approximation hypothesis - mostly heuristic in nature. That is why we evaluated multiple approaches to supersample generation and correction. The correction step involves a weighted mean over multiple candidates, each representing a correction as per the locally linear approximation at some original point.
| Step | Description |
|---|---|
| Supersample Generation | Multivariate normal distribution based on local covariances. |
| Supersample Generation | Uniform d-ball scaled with Cholesky decomposition of local covariances. |
| Supersample Generation | Uniform d-ball stretched to δ-expansion and scaled with Eigen decomposition of local covariances. |
| Correction Candidate Generation | Rotating supersample around original point by multiplying with covariance matrix and rescaling. Scales quadratic with eigenvalues of covariance matrix. |
| Correction Candidate Generation | Rotating supersample around original point by multiplying with Cholesky decomposition of covariance matrix and rescaling. Scales linearly with eigenvalues of covariance matrix. |
| Correction Candidate Weighting | Inverse Euclidean distance weighting. |
| Correction Candidate Weighting | Inverse Mahalanobis distance weighting as per local covariance of original point. |
| Correction Candidate Weighting | Inverse Mahalanobis distance weighting as per local covariance of supersampled point (estimated with original points). |
This gives 3·2·3=18 possible combinations of methods. Additional methods were evaluated but did not perform well enough to be considered.
Evaluation
Our evaluation showed that ID estimate quality of both angle- and distance-based estimates can be improved, albeit at the cost of computational effort due to largely increased neighborhood sizes.
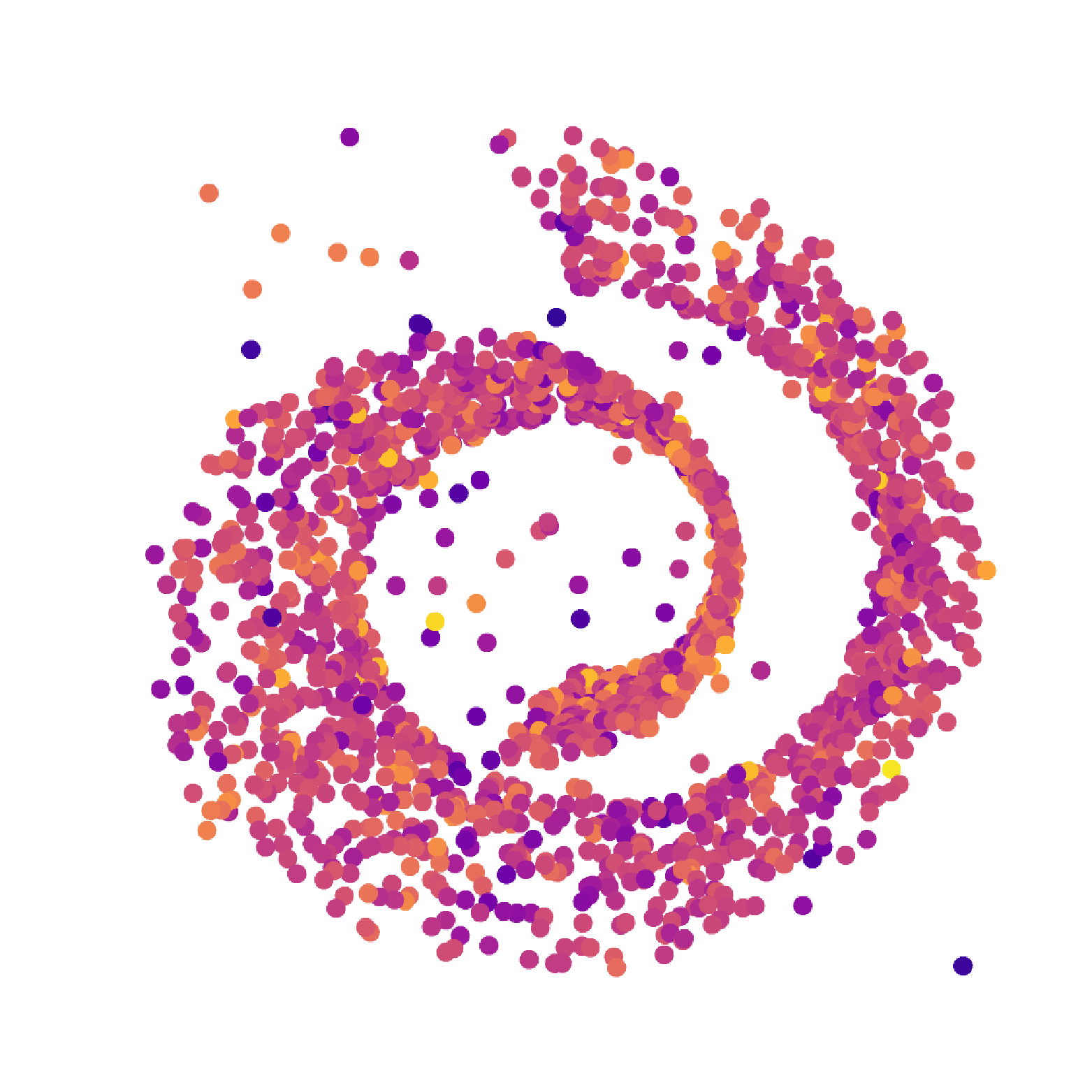
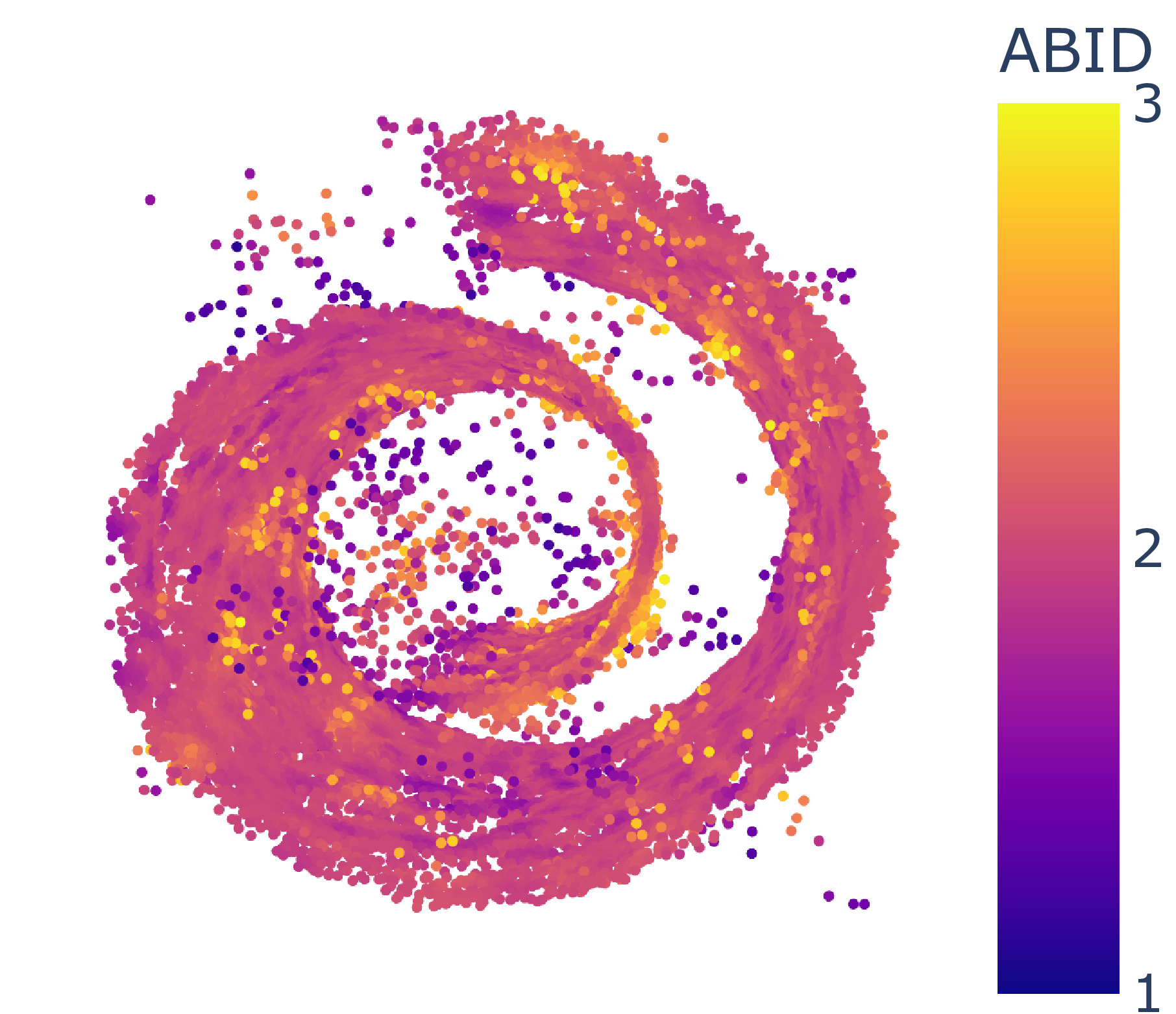
ABID estimates of Moebius band (δ=2, d=3) without (left) and with (right) MESS.
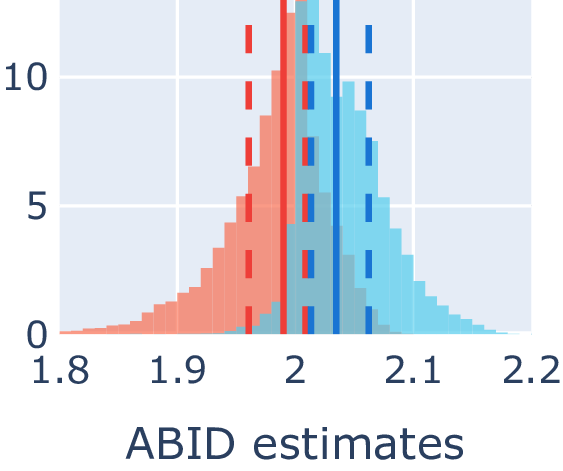
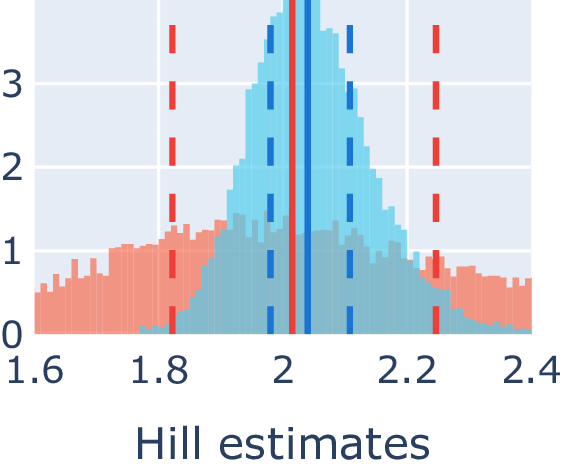
ID estimate distribution of Moebius band (δ=2, d=3) for angle-based ABID and distance-based Hill estimators without (orange) and with (blue) MESS.
The overlapping distributions blur out the local geometry well enough to lower the local LID estimate variance, strengthening the semantic correlation between estimates and geometry.
The most promising generation method are multivariate normal distributions, the best candidate weights are the Mahalanobis distance-based ones (all giving extremely similar results) and both candidate generation methods give acceptable results. Covariance-based correction constraints the estimates stronger onto the manifold than Cholesky decomposition-based correction which may or may not be preferred.
The best neighborhood sizes for covariance estimation appears to be the one which minimizes the (normalized) ID estimate variance. This coincides with the intuition of a narrow and “precise” ID estimate distribution.
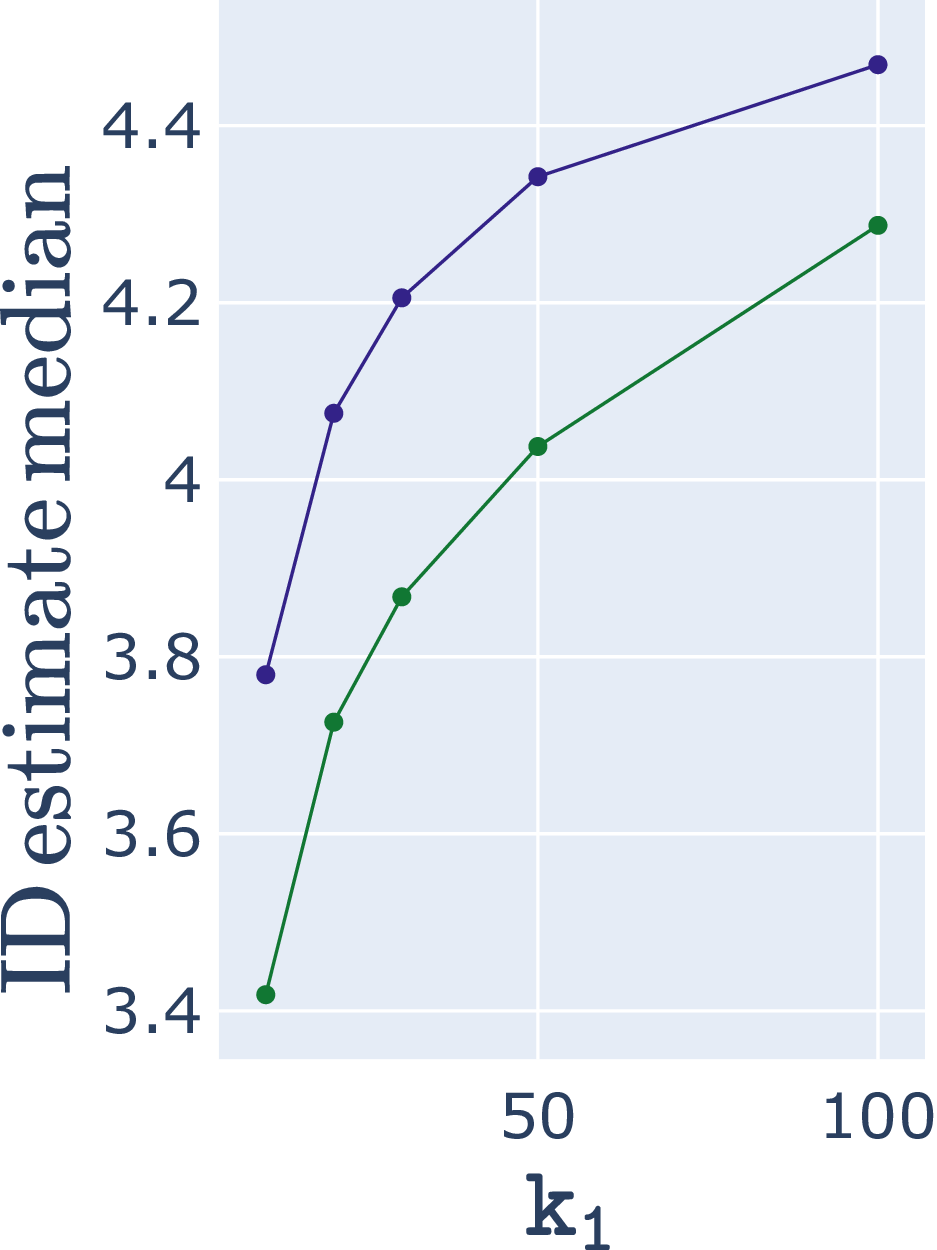
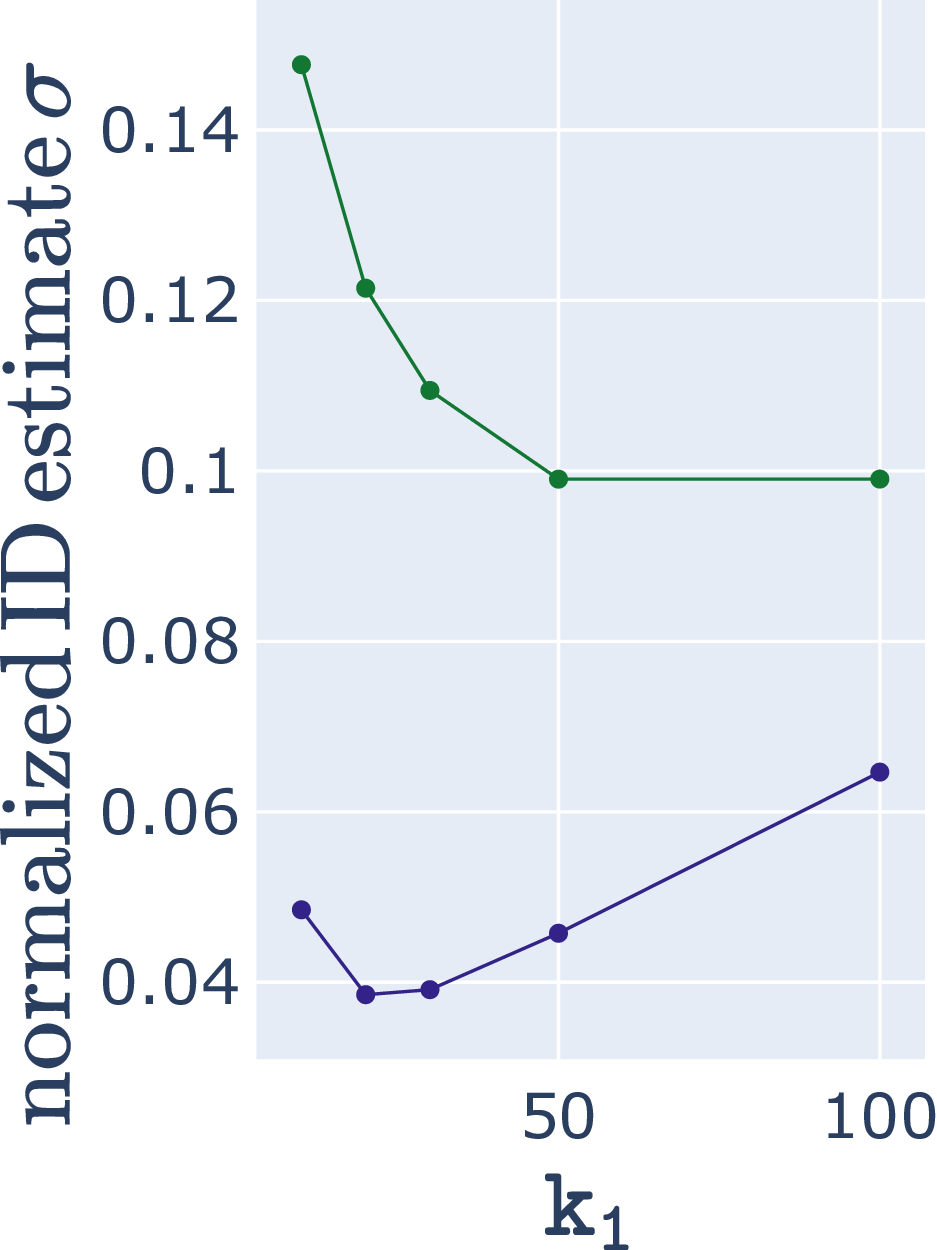
Median ID estimate and ID estimate variance for synthetic data set (δ=4, d=8) for angle-based ABID (blue) and distance-based Hill (green) estimators. Lowest variance is approximately at best median ID estimate.
Beyond LID Estimation
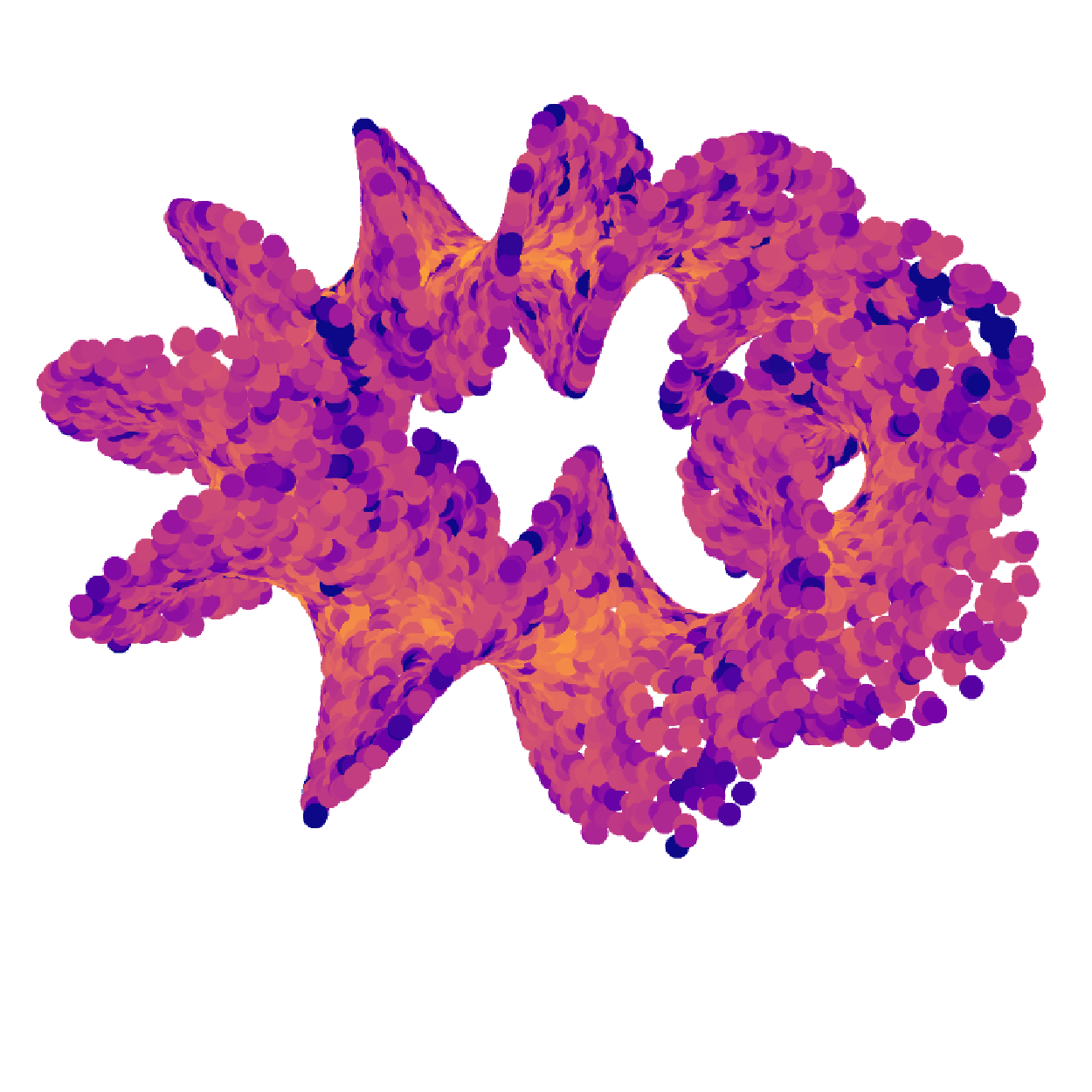
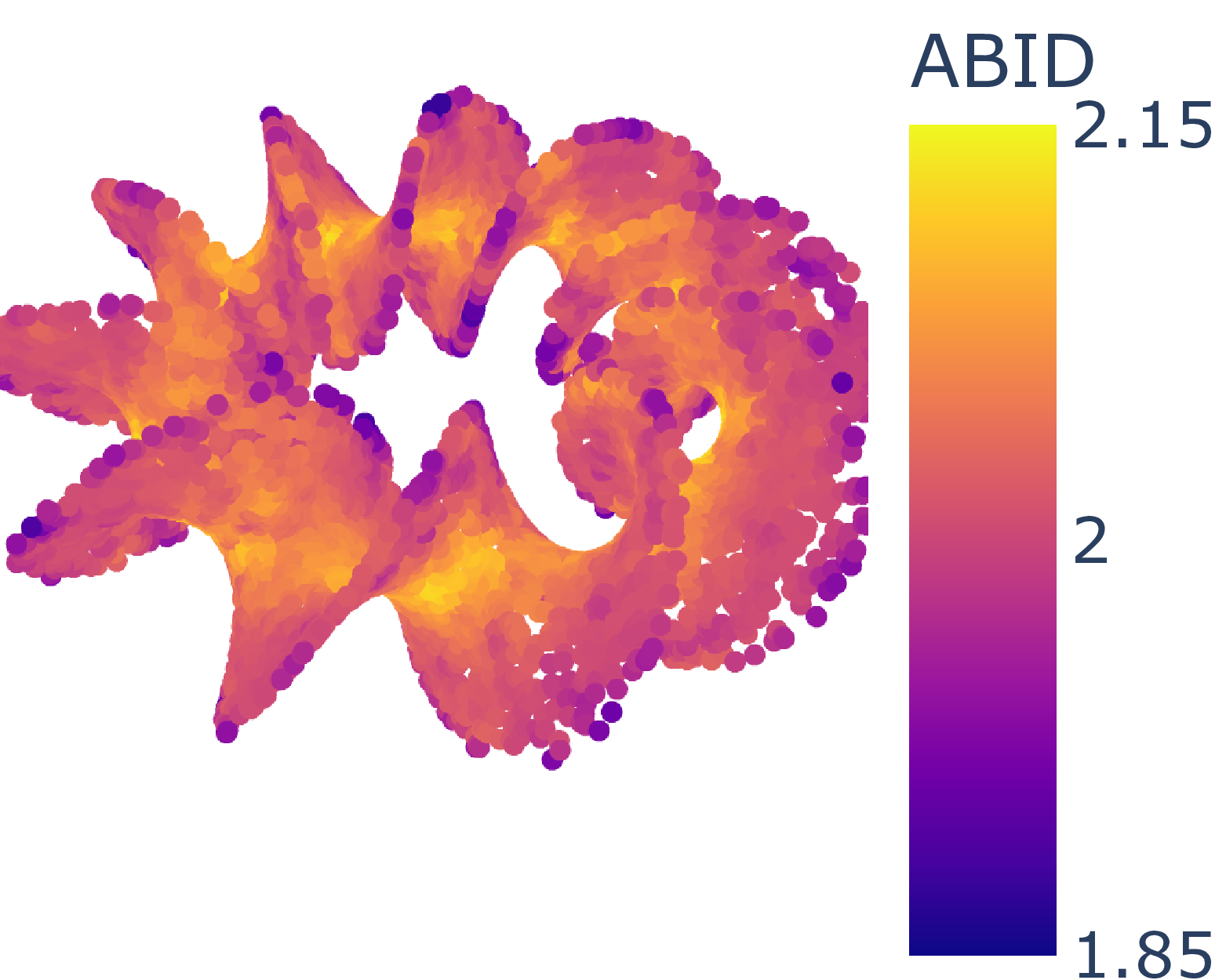
Data generated with MESS is faithful to an implicit manifold model (δ not required as parameter; no manifold learning required) and can be used in other tasks, like classification, as well. It is a potentially better suited over-/supersampling approach for manifold-based or -related methods than linear interpolation-based approaches like, e.g., SMOTE as it better preserves the manifold structure.

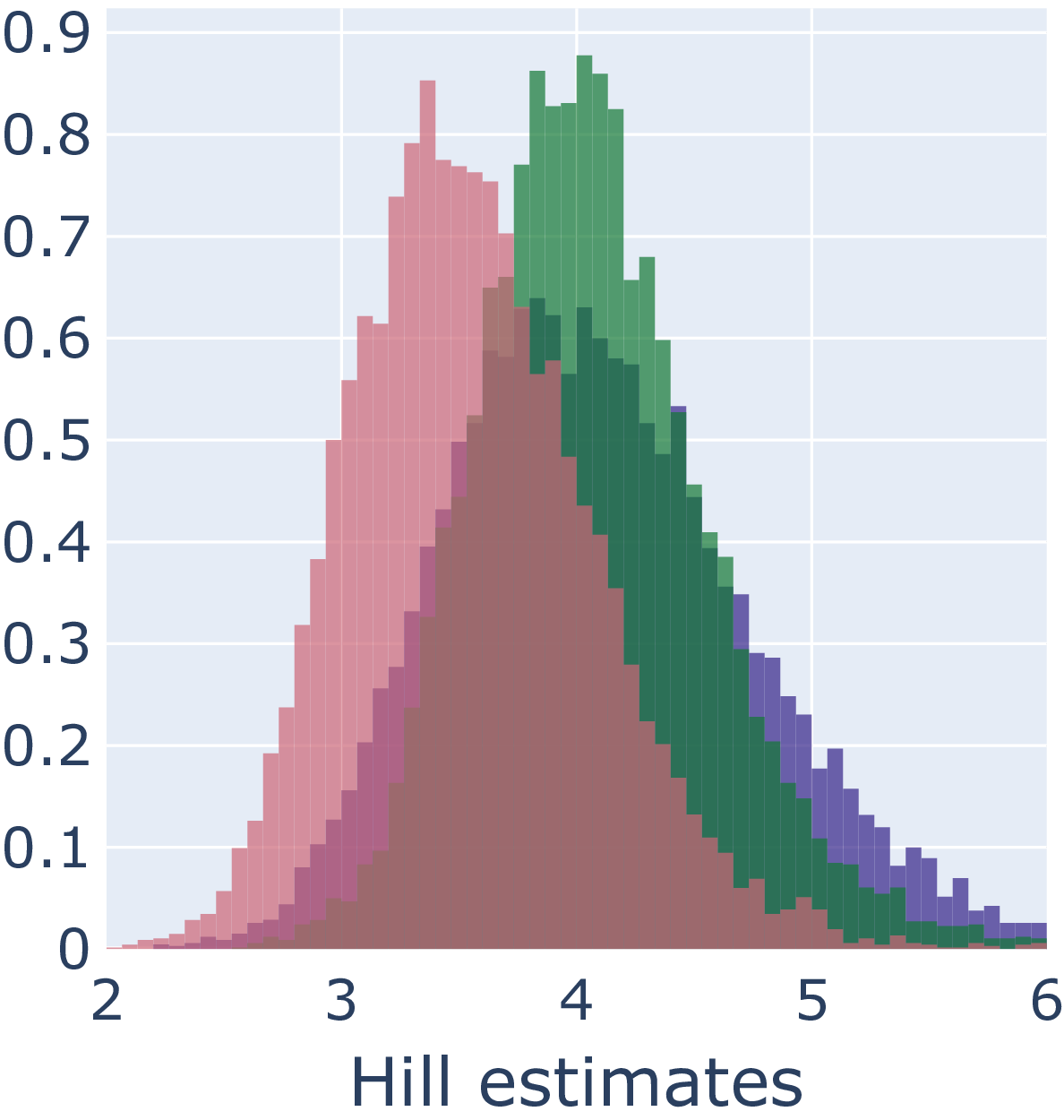
ID estimate distribution (δ=4, d=8) for angle-based ABID and distance-based Hill estimators without over-/supersampling (blue), with SMOTE oversampling (red), and with MESS supersampling (green).
Visual Examples
Below are two examples of MESS supersampling from real data sets. The first example shows supersamples based on MNIST instances and the second example a supersampled 3D scan with surface normals. In both cases, MESS generates supersamples on the manifolds and is capable of “filling gaps” in the original data, which would not be possible with SMOTE-style linear-interpolation.


Original MNIST instance (left), MESS supersamples (top row) and their respective nearest neighbor from the original data. Generated supersamples are distinct from original instances but in-distribution.
 |
 |
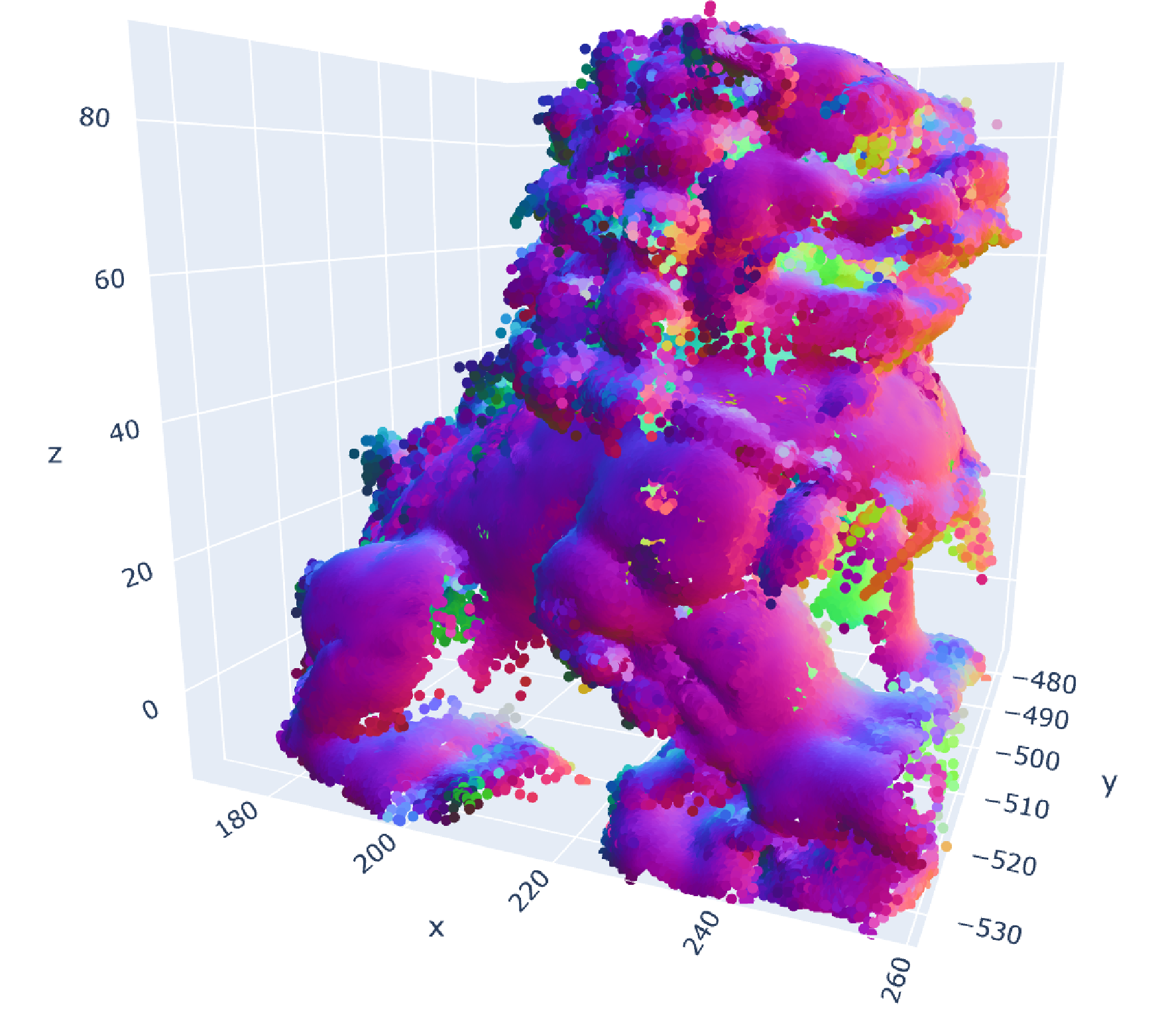 |
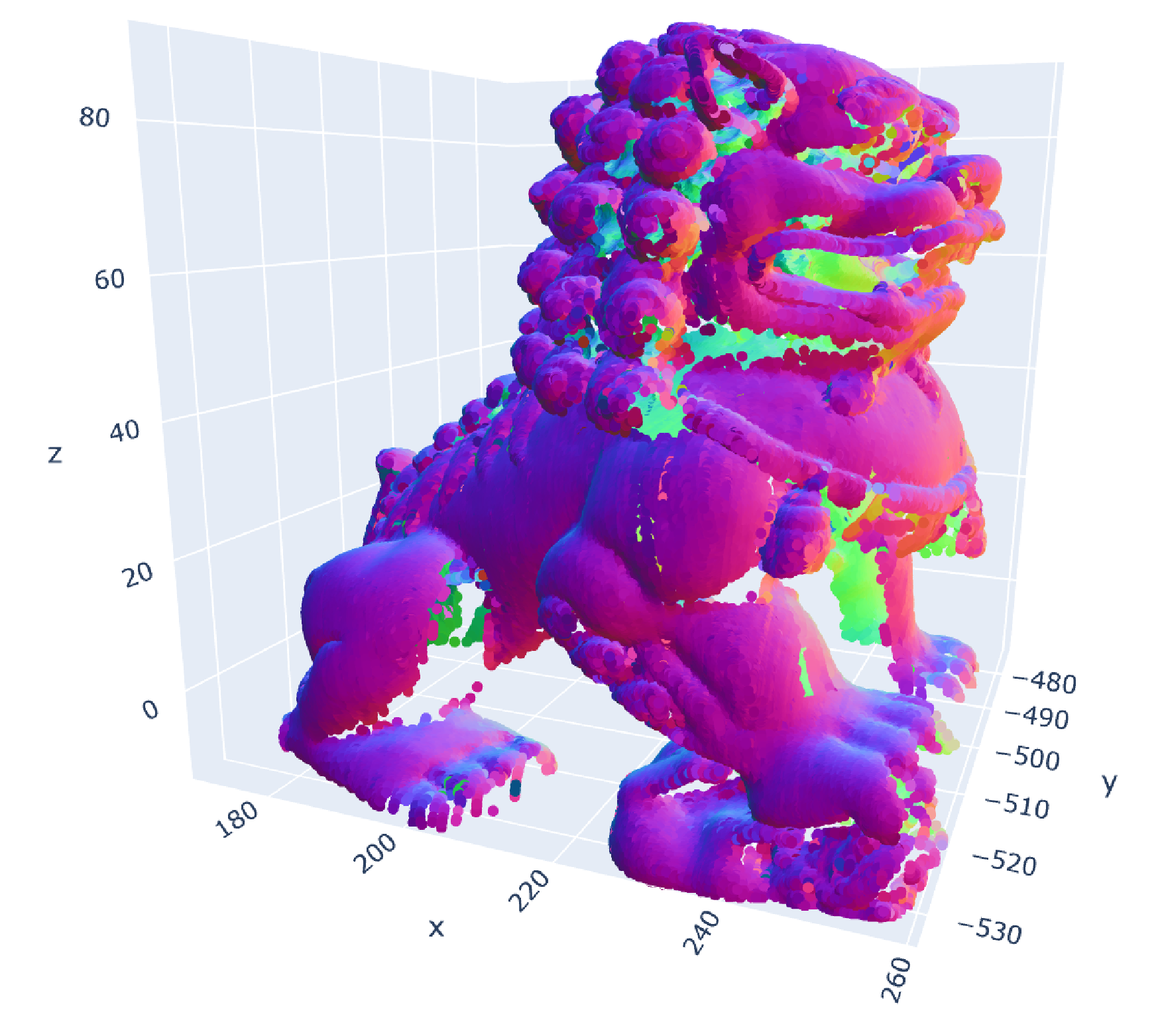
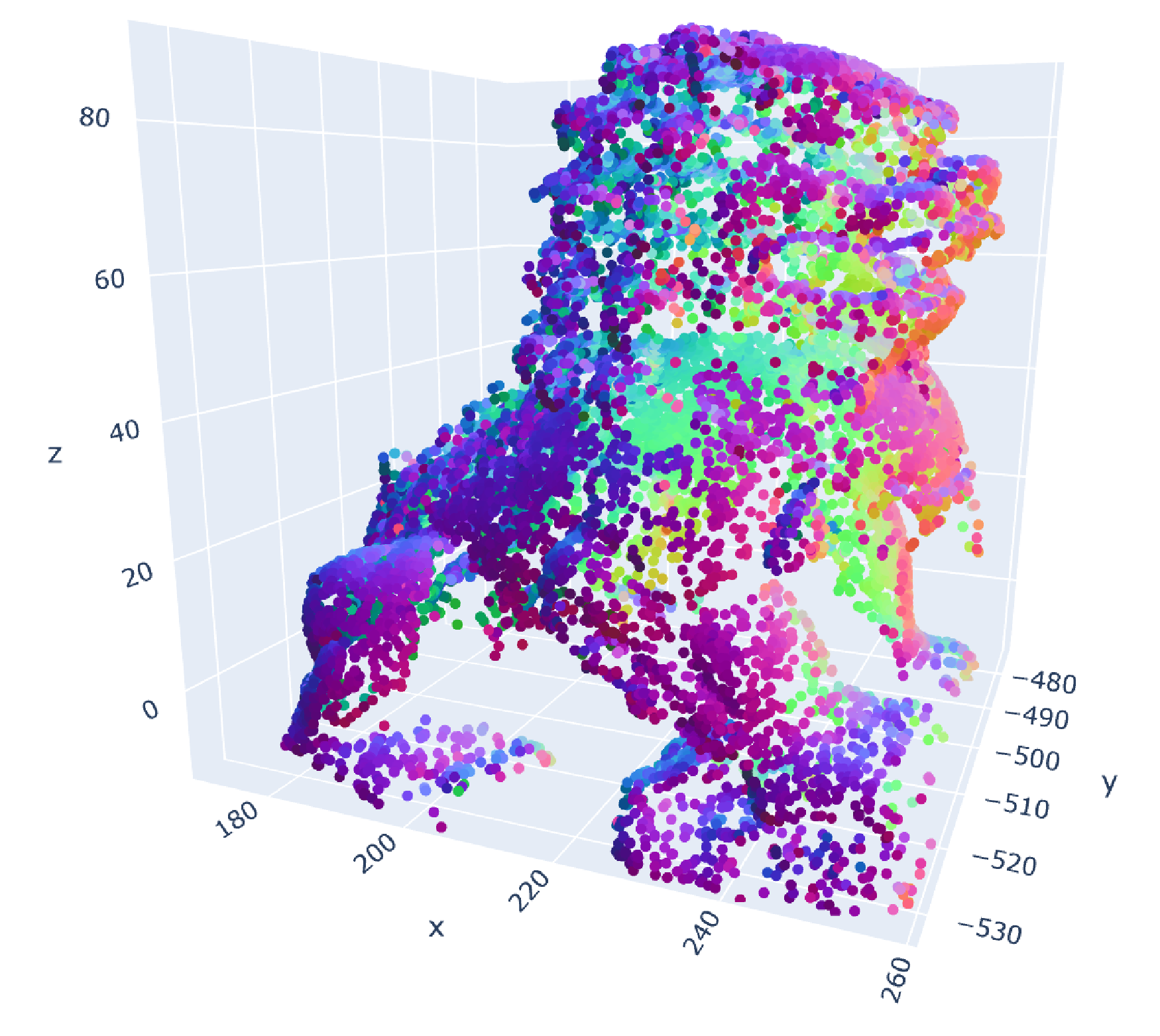
Original data (300k points, δ=2, d=6 due to surface normals) |
Sample of original data (15k points) |
MESS reconstruction (including surface normals) from sample (300k points) |

